Differential Calculus: From Practice to Theory

Credit: Cover of "Differential Calculus: From Practice to Theory" textbook, adapted from a work by Crockett Johnson, used with permission
Resource Description
Differential Calculus: From Practice to Theory covers all of the topics in a typical first course in differential calculus. Initially it focuses on using calculus as a problem solving tool (in conjunction with analytic geometry and trigonometry) by exploiting an informal understanding of differentials (infinitesimals). As much as possible large, interesting, and important historical problems (the motion of falling bodies and trajectories, the shape of hanging chains, the Witch of Agnesi) are used to develop key ideas. Only after skill with the computational tools of calculus has been developed is the question of rigor seriously broached. At that point, the foundational ideas (limits, continuity) are developed to replace infinitesimals, first intuitively then rigorously. This approach is more historically accurate than the usual development of calculus and, more importantly, it is pedagogically sound.
Learn moreFoundations in Sustainability Systems
Resource Description
Sustainability denotes one of the main future challenges of societies and the global community. Issues of sustainability range from energy and natural resources to biodiversity loss and global climate change. Properly dealing with these issues will be crucial to future societal and economic development. This course provides the theoretical background for the discussion and analysis of sustainability issues. Students will recognize specific sustainability issues, such as sustainable energy, as part of a more complex challenge of developing sustainable societies and systems, and against the background of the general meaning and implications of the conception of sustainability. Learn moreGame Theory: Lecture Notes
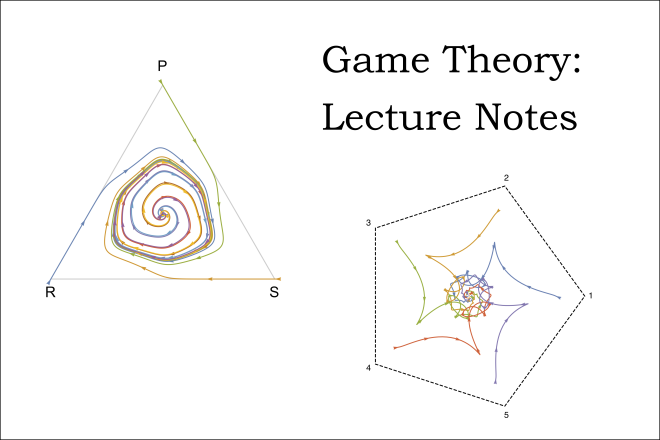
Credit: Image adapted from figures by Christopher Griffin and is licensed under CC BY-NC-SA 3.0 US
Resource Description
This is version two of a set of lecture notes for MATH 486, Penn State's undergraduate Game Theory course. Game Theory is the study of decision making under competition. The first truly mathematical study of Game Theory was initiated by Von Neumann and Morgenstern. John Nash (of A Beautiful Mind fame) added substantially to the field with his proof of the existence of equilibrium solutions for general sum games. Since then many mathematicians, economists, engineers and others have made substantial contributions to the study of games.
The lecture notes are loosely based on Luce and Raiffa's Games and Decisions: Introduction and Critical Survey. This is the same book John Nash used when he taught (or so I've heard). There are elements from Myerson's book on Game Theory (more appropriate for economists) as well as Morris' book on Game Theory. Naturally, I've also included elements from Von Neuman and Morgenstern's classic tome.
Learn moreGraph Theory: Lecture Notes

Credit: Image adapted from a figure by Christopher Griffin and is licensed under CC BY-NC-SA 3.0 US
Resource Description
This is version two of set of lecture notes for MATH 485, Penn State's undergraduate Graph Theory course. Graph Theory is the study of discrete mathematical structures composed of vertices (nodes) represented by dots and edges (links) represented by lines connecting the dots. Generally speaking, Graph Theory is a branch of Combinatorics but it is closely connected to Applied Mathematics, Optimization Theory and Computer Science. In its applied form, Graph Theory is used every day by Google and Microsoft in feeding you web information. It plays a major role in the functioning of your Facebook account and can be used to help analyze Twitter relationships. Graph Theory can also help track down criminals and makes your GPS function.
Learn moreLinear Programming: Lecture Notes
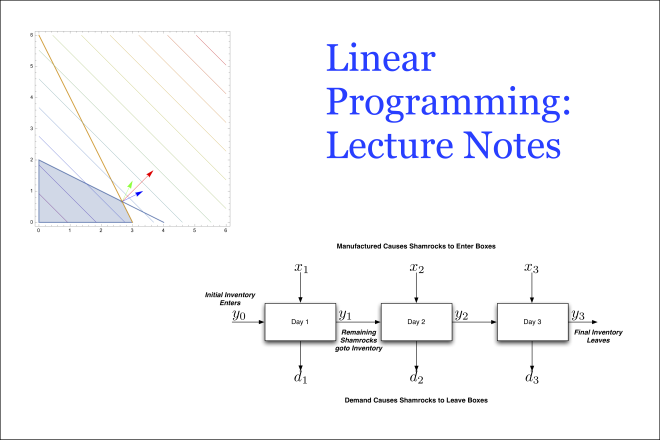
Credit: Image adapted from figures by Christopher Griffin and is licensed under CC BY-NC-SA 3.0 US
Resource Description
This is a set of lecture notes for Penn State’s undergraduate Linear Programming course.
The lecture notes are (roughly) based on the first 6 chapters of Bazaraa et al.’s Linear Programming and Network Flows book. This is a reasonably good book, written primarily by and for Industrial Engineers. However, it does not present major results in the standard theorem-proof style common to mathematical discourse. This set of notes corrects this situation by presenting the material in a format for presentation to a mathematics class.
Many of the proofs in this set of notes are adapted from the textbook with some minor additions. Additionally, I prefer to present maximization problems, while Linear Programming and Network Flows prefers the minimization format. I’ve modified all the proofs to operate on maximization problems. When used with the book, the student can obtain a complete set of proofs for elementary Linear Programming.
Learn moreNumerical Optimization: Lecture Notes
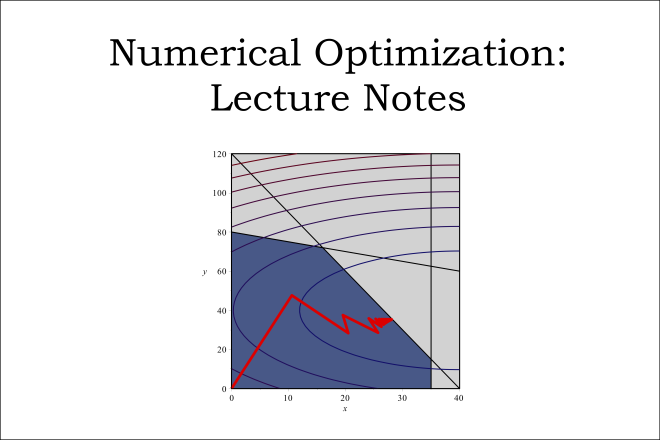
Credit: Image adapted from a figure by Christopher Griffin and is licensed under CC BY-NC-SA 3.0 US
Resource Description
This is a set of lecture notes for MATH 555, Penn State's graduate Numerical Optimization course. Numerical Optimization is the study of maximizing or minimizing functions through numerical techniques. Generally, it's rare to optimize anything other than through numerical techniques (unless of course you're talking about something really simple). Numerical optimization is used every day and is built on techniques from multi-variable calculus, optimization theory (obviously) numerical linear algebra (for algorithm efficiency) and other branches of mathematics.
Learn moreTechniques of Calculus, I

Credit: Image adapted from a figure in Applied Calculus: Principles and Applications by Robert Gibbes Thomas, public domain
Resource Description
A Jupyter notebook companion for a first course in Calculus, including a review of Precalculus concepts.
Learn more
